Question

Which of the following functions best describes this graph?

A. y=x^2+9x+18
B. y=(x-3)(x-6)
C. y=x^2-2x+4
D. y=(x+5)(x-4)

Answer 1

Heyyyy!!!!! I'm going to say choice A

Answer 2

A.
`y=x^2+9x+18`

Explanation:

By the given graph,

The function is intersecting x-axis at - 3 and - 6,

Thus, the x-intercepts of the given function must be (-3,0) and (-6,0),

Now, In option A,

The function is,

`y=x^2+9x+18`

For x-intercept y = 0,

`x^2+9x+18=0`

`x^2+6x+3x+18=0`

`x(x+6)+3(x+6)=0`

`(x+3)(x+6)=0`

`\implies x = -3\text{ or }x = -6`

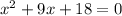
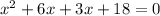
⇒ x-intercepts are (-3,0), (-6,0)

⇒ The function
`y=x^2+9x+18` describes the given graph,

Now, In option B,

The function is,

`y=(x-3)(x-6)`

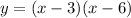
For x-intercept y = 0,

`(x-3)(x-6)=0`

`\implies x = 3\text{ or }x = 6`

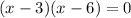
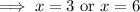
⇒ x-intercepts are (3,0), (6,0)

⇒ The function
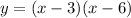`y=(x-3)(x-6)` does not describe the given graph,

Now, In option C,

The function is,

`y=x^2-2x+4`

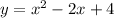
For x-intercept y = 0,

`y=x^2-2x+4=0`

`(x-2)^2=0`

`\implies x = 2`

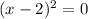
⇒ x-intercept is (2,0),

⇒ The function
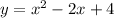`y=x^2-2x+4` doesn't describe the given graph,

Now, In option D,

The function is,

`y=(x+5)(x-4)`

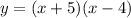
For x-intercept y = 0,

`(x+5)(x-4)=0`

`\implies x = -5\text{ or }x = 4`

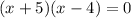
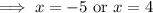
⇒ x-intercepts are (-5,0), (4,0)

⇒ The function
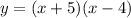`y=(x+5)(x-4)` does not describe the given graph.