Question

Use the polynomial 2x6−6x3−5x7+7x−11x2+35 to answer the question. What is the leading coefficient of this polynomial?

Answer 1

Once again if the numbers after x are supposed to be exponents(the raising power) then the answer will be -5

Answer 2

-5

Explanation:

In a polynomial, the coefficient of the term with the highest degree or power is called the leading coefficient of the polynomial.

We are given a polynomial
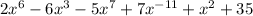`2x^6-6x^3-5x^7+7x^(-11)+x^2+35`. It is a good idea to rearrange this polynomial with powers in a descending order.

`-5x^7 +2x^6-6x^3+x^2+7x^(-11) +35`

As we can see the highest power being 7 so the coefficient of the term with the power 7 is -5. Therefore, -5 is the leading coefficient.