Question

Find all values of theta if theta is in the interval [0degrees,360degrees) and has the given function value

sec theta= -2

Answer 1

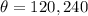`\theta = 120, 240`, in degrees

Explanation:

The secant of an angle is given by:

`\sec{\theta} = (1)/(cos(\theta))`

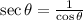
In this question:

`\sec{\theta} = -2`

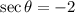
So

`(1)/(cos(\theta)) = -2`

`-2cos(\theta) = 1`

`cos(\theta) = -(1)/(2)`

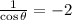
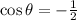
In the first quadrant, the angle that has cosine of 1/2 is 60º.

The cosine is negative in the second and in the third quadrant.

The equivalent angle to 60º in the second quadrant is of 180º - 60º = 120º.

The equivalent angle to 60º in the third quadrant is of 180º + 60º = 240º

So the values of
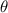`\theta` in the interval are:

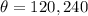`\theta = 120, 240`, in degrees