Question

Use the polynomial 3x2−4x11+4x4−2x10−5+8x8 to answer the question. What is the degree of this polynomial?

Answer 1

If the numbers after x are exponents(power) the the answer would be 8 has the degree but if the numbers are not raising to the power then I'm not quite sure.

Answer 2

For this case we have a polynomial P (x) of the form:

`P(x)=ax^n+...+bx^i+...+cx^3+dx^2+ex+f`

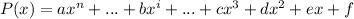
Where:

• a, b, c, d, e and f: They are the coefficients of the terms of the polynomial

• x: It is the variable associated with the polynomial

• n, i, 3,2,1 and 0: Are the exponents. Where n is the greatest exponent.

In this way, we can say that the degree of the polynomial P (x) is n.

Then, given:

`Q(x)=3x^2-4x^(11)+4x^4-2x^(10)-5+8x^8`

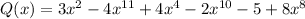
We order the polynomial from highest to lowest exponent:

`Q(x)=-4x^(11)-2x^(10)+8x^8+4x^4+3x^2-5`

In this way, it can be seen that the largest exponent is 11.

Thus, the degree of the polynomial
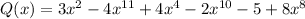`Q(x)=3x^2-4x^(11)+4x^4-2x^(10)-5+8x^8` is 11.

Answer:

The degree of the polynomial is 11.