Question

Over what interval is the function differentiable? Y=3/2(x-1)

Answer 1

The interval where the function is diffrentiable is

`[-\infty,1)\ \bigcup\ (1,\infty]`

Solution-

The given expression is,

`y=(3)/(2(x-1))`

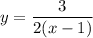
The function will be differentiable where it is continuous and it will not be differentiable, where the function is not continuous.

The function continuous everywhere except at x = 1, because

`\Rightarrow 2(x-1)=0\\\\\Rightarrow x-1=0\\\\\Rightarrow x=1`

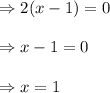
at x = 1, its limit does not exist.

Therefore, apart from x=1, this function is differentiable everywhere. The interval will be

`[-\infty,1)\ \bigcup\ (1,\infty]`