Question

How to solve for x and y

Answer 1

The values of x and y are 20° and 30, respectively.

Solution-

As in the given triangle all the angles are same so it must a equilateral triangle.

In an equilateral triangle all the measurements of the angles and side length are same. The measurement of the angels are 60°.

As given in the question one side length is 46, so all the side length are same.

So,

`\Rightarrow y+16=46\\\\\Rightarrow y=46-16\\\\\Rightarrow y=30`

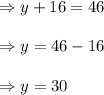
We know that an exterior angle of a triangle is equal to the sum of the opposite interior angles. 80° is the exterior angle opposite to x and one angle of triangle at the top vertex.

`\Rightarrow 80^(\circ)=x+60^(\circ)`

`\Rightarrow x=80^(\circ)-60^(\circ)`

`\Rightarrow x=20^(\circ)`

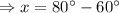
Therefore, the values of x and y are 20° and 30, respectively.