Question

(a) The diagram shows a circle, centre 0. AB and CD are chord.

Given that OM = 8 cm, NT = 3 cm, AB = 30 cm.

(1) Calculate the radius
(2) Calculate the length of CD​

Answer 1

1) Radius = 17 cm

2). CD = 19.3 cm

Explanation:

1). O is the center of the given circle.

By joining the center and point A located at the circumference of the circle,

OA = radius of the circle.

Length of chord AB = 30 cm

"Line from the center of a circle to the chord inside the circle is a perpendicular bisector of the chord"

By the given property, OM equally divides the chord AB.

AM = MB

AM =
`(1)/(2)(AB)`

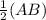
AM =
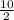`(10)/(2)` = 5 cm

By applying Pythagoras theorem in ΔOAM,

AO² = OM² + AM²

AO² = 8² + 15²

AO = √289

AO = 17 cm

Therefore, radius of the circle = 17 cm

2). Since, OT, OC and OA are the radii of the given circle,

OT = OC = OA = 17 cm

ON = OT - NT

= 17 - 3

= 14 cm

By applying Pythagoras theorem in ΔOCM,

OC² = ON² + CN²

17² = 14² + CN²

CN =
`√((17^2-14^2))`

=
`√(93)`

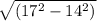
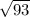
= 9.64 cm

Since, CD = 2(CN)

CD = 2 × 9.64

= 19.29 cm

≈ 19.3 cm