Question

in a poll, 52% of households have two or more cars.The poll has a margin of error +4 percentage points.Write and Solve an absolute value inequality to find the least and greatest percent of households that have two or more cars.

Answer 1

`48\leq x\leq 56`.

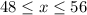Explanation:

Let x represent percent of households with two or more cars.

We will use margin of error formula to solve our given problem.

`|\text{Actual}-\text{Ideal}|\leq\text{Tolerance}`

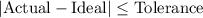
Substitute the given values:

`|x-52|\leq4`

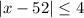
Using absolute value property
`|u|\leq a`, then
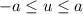`-a\leq u\leq a`, we will get:

`-4\leq x-52\leq4`

`-4+52\leq x-52+52\leq4+52`

`48\leq x\leq 56`

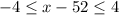
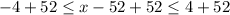
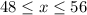
Therefore, our required inequality would be
`48\leq x\leq 56` and least percent is 48% and greatest percent is 56%.

Answer 2

Let the households with cars be represented by = c

As given 52% households have 2 or more cars and margin of error is +- 4%

The equation becomes

`|c-52|\leq4`

Solving this we get,

`-4\leq c-52\leq4`

`-4+52\leq c\leq 4+52`

`48\leq c\leq56`

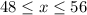Hence, the least percent is 48% and greatest percent is 56%