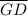Question

The figure shows triangle ABC with medians A F, BD, and CE. Segment A F is extended to H in such a way that segment GH is congruent to segment AG. ​Which conclusion can be made based on the given conditions?

Segment GF is parallel to segment EB.
Segment EG is parallel to segment BH.
Segment BH is congruent to segment HC.
Segment EG is congruent to segment GD.

ONLY answer if you confidently know, ​please.

Answer 1

I would say that the answer is probably Segment EG is parallel to segment BH. Hope this helped!

-TTL

Answer 2

From given Conditions we conclude that
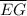`\overline{EG}` is parallel to
`\overline{BH}`

Explanation:

Given:
`\overline{FA}` ,
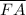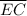`\overline{EC}` and
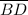`\overline{BD}` are medians of ΔABC.

`\overline{AG}\:=\:\overline{GH}`

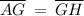
Option 1:

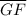`\overline{GF}` is not parallel to
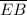`\overline{EB}` because on extending both segment they are intersecting at A but parallel lines never intersects.

Option 2:

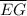`\overline{EG}` is parallel to
`\overline{BH}` because E is mid point of
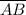`\overline{AB}` and G is mid point of
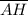`\overline{AH}` then according to Mid Point Theorem
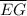`\overline{EG}` is Parallel to
`\overline{BH}`.

Option 3:

`\overline{BH}` is not congruent to
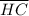`\overline{HC}`. It is clear from figure.

Option 4:

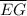`\overline{EG}` is not congruent to
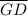`\overline{GD}`. Since from above option
`\overline{BH}` is not congruent to
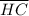`\overline{HC}` then using Mid Point theorem in ΔABH and ΔAHC.

We get,

In ΔABH
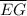`\overline{EG}` is parallel to
`\overline{BH}` &
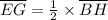`\overline{EG}=(1)/(2)*\overline{BH}` ....... Eqn (1)

Similarly,

In ΔAHC

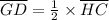`\overline{GD}=(1)/(2)*\overline{HC}` ........ Eqn (2)

So, from eqn (1) & (2)

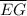`\overline{EG}` ≠
`\overline{GD}`