Answer:
From the given graph:
the coordinates of triangle RST are;
R= (2, 1),
S= (2,-2),
T= (-1,-2)
Given: Scale factor =
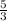 and center of dilation at (2,2)
and center of dilation at (2,2)
The mapping rule for the dilation applied to the triangle as shown below:
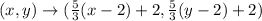 ; where k represents the scale factor i.e,
; where k represents the scale factor i.e,
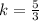 or we can write it as ;
or we can write it as ;
For R=(2, 1)
The image R' =
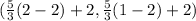
⇒ R'=

Similarly for S= (2, -2) and T= (-1,-2)
therefore, the image of S'=
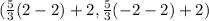
⇒ S'=

The image of T' =
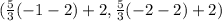
⇒T' =

Now, labelling the image of triangle R'S'T' as shown in the figure given below