The interval given was 33% to 37%
This means that subtracting the margin of error from the percentage of the population that visit the library once a year gives the lower end and adding the margin of error to the percentage of the population that visit the library once a year gives the upper end
Let x denote margin of error and y denotes the percentages of the population that visit the library once a year
we can get the following equations and solve for the values of x and y
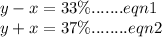
Adding eqn1 and eqn2 to gives
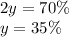
Putting the value of y into any of the equations
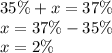
Thus, the margin of error is
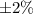
Therefore we enter 2 in the box