ANSWER
The line that is parallel to
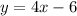 through
through
 is
is
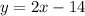 .
.
Step-by-step explanation
The equation that is parallel to the line
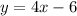 has a slope that is equal to the slope of this line.
has a slope that is equal to the slope of this line.
By comparing this equation to the general slope intercept form,
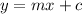 ,this line has slope
,this line has slope
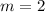 .
.
Hence the line parallel to this line also has slope
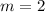 .
.
Let
 be the equation of the line parallel to the line
be the equation of the line parallel to the line
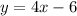
We can substitute
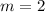 to obtain;
to obtain;
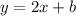
If the line passes through the point
 ,then this point must satisfy its equation.
,then this point must satisfy its equation.
We substitute
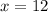 and
and
 to obtain;
to obtain;

We this equation for
 .
.

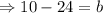

We substitute this value of
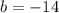 in to
in to
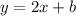 to get;
to get;
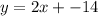 .
.
Hence the equation of the line that is parallel to
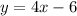 through
through
 is
is
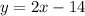 .
.