Answer:
Option C - 420
Explanation:
Given : Objective function, P, with the given constraints
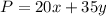
Constraints,
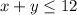
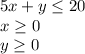
To find : What is the maximum value
Solution :
First we plot the graph through the given constrains.
As they all move towards the origin the common region of the equations is given by the points (0,0), (0,12), (2,10), (4,0)
Refer the attached figure.
So, we put all the points in P to, get maximum value.
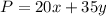
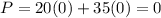
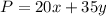
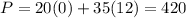
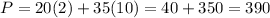
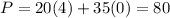
Therefore, The value is maximum 420 at (0,12)
So, Option C is correct.