Question

The table shows the input and output of a function Table(input:3,4,6,11. Output:5,7,11,21) (a) Explain what makes this set of data a function. (B) what could cause this set of data to not be a function? Provide a specific example to support your statement and explain throughly. (c) write an equation, in function nation, that would fit in the inputs and outputs in the table. Show your work that proves your equation is true for the given data. PLEASE HELP ITS DUE TODAY!!!l

Answer 1

(a) The data set is a function, since for each input value {3,4,6,11} there is a single output value {5,7,11,21}

(B) A function is a mathematical relationship that associates one or more inputs with a single output value. So that the data set is not a function, there should be - for one or more values ​​of the input - more than one output.

for example, if for the input value {3} there were two outputs {5, -5} then, the data set would not be a function.

The frelation
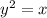`y ^ 2 = x` is not a function because:

When x = 1, y = +1 and y = -1.

(c) The set of data provided can be represented by the equation of a line of the form y = mx + b

The slope is:

`m=(y_2-y_1)/(x_2-x_1)`

`m =(7-5)/(4-3)`

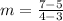
m = 2

`b = y_1-mx_1`

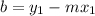
b = 5 - 2*3

b = -1

Then, the function is:

y = 2x-1

You can substitute any of the points shown in the equation and check that equality is satisfied, for example:

(11 , 21)

y = 2 (11) -1

y = 22-1

y = 21. The equation is satisfied. The same goes for the rest of the values.