Question

Steve can complete the 100m dash in 10 seconds while Paul can run it in 12 seconds. How does Steve's time compare to Paul's? A. Steve is 1⁄2 as fast as Paul B. Steve is 1⁄2 slower than Paul C. Steve is 5⁄6 as fast as Paul D. Steve is 5⁄6 slower than Paul

Answer 1

C. Steve is 5⁄6 as fast as Paul

Explanation:

For, Steve,

Distance = 100 m,

Time = 10 seconds,

Now, For Paul,

Distance = 100 m,

Time = 12 seconds,

Since, the distance for both are same,

Thus,

`\frac{\text{Steve's time}}{\text{Paul's time}}=(10)/(12)`

`=(5)/(6)`

`\implies \text{Steve's time}=(5)/(6)\text{ of Paul's time}}`

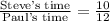
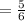
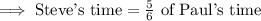
Hence, Steve's time is 5⁄6 of the time taken by Paul.

Option C is correct.

Answer 2

10/12

5/6

Steve is 5/6 as fast as Paul

Choice C