Answer:
The equation of the perpendicular bisector line
5 x - 2 y + 31 =0
Explanation:
Explanation:-
Given points are ( 0,1) and (-10,5)
The Midpoint of given two points
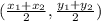
(-5 , 3)
The Slope of the line
m =
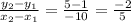
The perpendicular slope
=
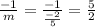
The equation of the perpendicular bisector line
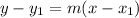
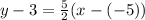
2 y - 6 = 5( x +5)
5 x + 25 -2y +6 =0
5 x - 2 y + 31 =0