Question

what is tye minimum value for P=x-4y over the feasibility region defined by the constraints shown above?

Answer 1

The correct option is: -30

Explanation:

According to the given graph, the the leftmost vertex of the feasibility region is the intersecting point of lines
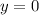`y=0` and
`y= 3x+2`

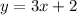
Now, solving the above two equations, we will get.......

`0=3x+2\\ \\ 3x=-2\\ \\ x=-(2)/(3)`

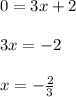
So, the co ordinate of the leftmost vertex will be:
`(-(2)/(3),0)`

From the given graph, the other vertices are:
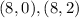`(8,0), (8,2)` and
`(2,8)`

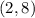
Given objective function is:
`P= x-4y`

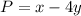
Now, we need to find the value of that objective function at each vertex. So....

For
`(-(2)/(3),0)` ,
`P= -(2)/(3)-4(0)=- (2)/(3) \approx -0.67`

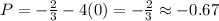
For
`(8,0)` ,
`P=8-4(0)=8`

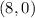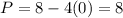
For
`(8,2)` ,
`P=8-4(2)=8-8=0`

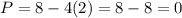
For
`(2,8)` ,
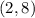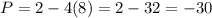`P=2-4(8)=2-32=-30` (Minimum)

Thus, the minimum value of the objective function will be -30.