Question

PRE CALC HELP 50 PTS

Answer 1

`\sec( (x)/(3) ) + 4 > 2 - \sec( (x)/(3) ) \\ 2 \sec( (x)/(3) ) > - 2 \\ \sec( (x)/(3) ) > - 1 \\ \boxed{y = \sec( (x)/(3) )} \\ \boxed{y = - 1}`

B) is the right answer.

Answer 2

B

Explanation:

We want to solve the inequality:

`\displaystyle \sec\Big((x)/(3)\Big)+4>2-\sec\Big((x)/(3)\Big )`

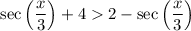
First, we can add sec(x/3) to both sides:

`\displaystyle2 \sec\Big((x)/(3)\Big)+4>2`

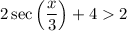
Subtracting 4 from both sides yields:

`\displaystyle 2\sec\Big((x)/(3)\Big)>-2`

And dividing both sides by 2 yields:

`\displaystyle \sec\Big((x)/(3)\Big)>-1`

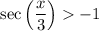
Therefore, we can graph the following two functions:

`\displaystyle y=\sec\Big((x)/(3)\Big)\text{ and } y=-1`

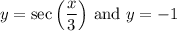
Where our solutions will be all the intervals where y = sec(x/3) is above the line y = -1.