ANSWER
The correct answer is D
EXPLANATION
To graph the inequality
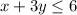
we first graph the corresponding equation,
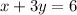
We then test the origin to determine which half-plane to shade the inequality,
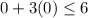
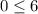
The above statement is true so we shade the lower half plane.
Next, we graph

By first graphing the corresponding equation,
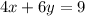
Then we test the origin again,
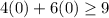
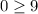
This statement is false, so we shade the upper half plane
Next, we graph,
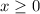
Draw the vertical line
 and shade to the right.
and shade to the right.
Finally, we graph,
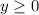
Draw the horizontal line
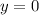 and shade the upper region.
and shade the upper region.
the intersection of all the shaded regions is called the feasible region.
The four vertices of the feasible region are

Hence the correct answer is D