Answer:
(1+2i)(1-2i)
Explanation:
Following are the pairs of the complex number:
(1+2i)(8i),
(1 + 2i)(2 – 5i)
(1+2i)(1-2i) and (1+2i)(4i)
We have to check which pair out of these is a real number product, which means which pair do not contain terms consisting of "i".
A.
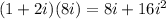
=

B.
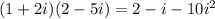
=
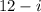
C.
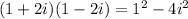
=

D.
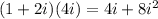
=

Since, A,B,D contains the term "i" which means they are not real valued, therefore option C that is (1+2i)(1-2i) has a real number product.