Question

Which expression represents the polynomial 2−6x3+5x5−x2 rewritten in descending order, using coefficients of 0 for any missing terms? 5x5−6x3+x2+0x+2

5x5+0x4−6x3+x2+0x−2
5x5+6x3−x2−2
5x5+0x4−6x3−x2+0x+2
−5x5−6x3+x2+0x+2
−5x5+6x3−x2+2

Answer 1

hich expression represents the polynomial 2−6x3+5x5−x2 rewritten in descending order, using coefficients of 0 for any missing terms? 5x5−6x3+x2+0x+2

5x5+0x4−6x3+x2+0x−2

5x5+6x3−x2−2

5x5+0x4−6x3−x2+0x+2

−5x5−6x3+x2+0x+2

−5x5+6x3−x2+2

Step-by-step explanation:

mamamamamamamam mark me as ace plz ☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)☜(ﾟヮﾟ☜)⊙.☉⊙.☉⊙.☉♨_♨(╯°□°）╯︵ ┻━┻¯\_(ツ)_/¯¯\_(ツ)_/¯¯\_(ツ)_/¯¯\_(ツ)_/¯¯\_(ツ)_/¯ಥ_ಥಥ_ಥಥ_ಥ✔✔✔✔

Answer 2

• 5x⁵ + 0x⁴ − 6x³ − x² + 0x + 2

Step-by-step explanation:

This is the expression of the original polynomial, showing the exponents of the variables properly:

• 2 − 6x³ + 5x⁵ − x²

Writing a polynomial in descending order means to arrange the terms such that the first term has the variable with the highest exponent, the second term contains the variable raised to a lesser exponent, and so on until the final term which is the constant term.

Mathematically that is:

`a_nx^(n)+a_(n-1)x^(n-1)+a_(n-2)x^(n-2)+...+a_1x+a_0`

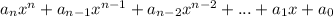
Hence, the terms of the polynomial in descending order are:

• 5x⁵ − 6x³ − x² + 2

There you see that the terms with x⁴ and x are missing. So, you can include those terms using 0 as coefficient:

• 5x⁵ + 0x⁴ − 6x³ − x² + 0x + 2

And that is the answer.