Answer:
 over 2a
over 2a
Step-by-step explanation: To solve this problem, we will use the method of completing the square.
In this problem, a, b, and c are integers. So to complete the square, it's important to understand that we can't have a coefficient on the x² term so we divide both sides of the equation by a to get


Next we move the
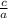 to the right side of the equation by subtracting
to the right side of the equation by subtracting
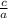 from both sides and we have
from both sides and we have
 To complete the square, it's important to understand that we take half the coefficient of the middle terms squared. Since the coefficient of the middle term is a fraction,
To complete the square, it's important to understand that we take half the coefficient of the middle terms squared. Since the coefficient of the middle term is a fraction,
 we can take half of it by simply doubling the denominator to get
we can take half of it by simply doubling the denominator to get
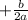 and when squaring
and when squaring
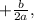 remember to square both the numerator and denominator so we get
remember to square both the numerator and denominator so we get
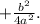
So we add
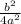 to both sides of the equation. Next, remember that our trinomial on the left factors as a binomial squared and the binomial uses half the coefficient of the middle term of the trinomial. So we use half of
to both sides of the equation. Next, remember that our trinomial on the left factors as a binomial squared and the binomial uses half the coefficient of the middle term of the trinomial. So we use half of
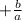 which is
which is
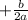 and we have
and we have
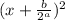 .
.
On the right, when adding
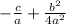 , our common denominator is
, our common denominator is
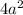 so we multiply top and bottom of
so we multiply top and bottom of
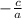 by
by
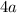 to get
to get
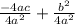 which we can rewrite as
which we can rewrite as
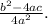 Note that we have switched the order of the -4ac and the b². Don't get thrown off here.
Note that we have switched the order of the -4ac and the b². Don't get thrown off here.
To get rid of the square on the left side of the equation, we square root both sides so on the left we have
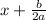 and on the right remember to use + or - and also remember that when square rooting a fraction, we must square root both the numerator and the denominator so we have
and on the right remember to use + or - and also remember that when square rooting a fraction, we must square root both the numerator and the denominator so we have
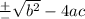 over 2a.
over 2a.
To get x by itself, subtract
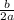 from both sides and we have
from both sides and we have
 over 2a.
over 2a.
Remember the answer to this problem. It's called the quadratic formula. The beauty of the quadratic formula is as long as your quadratic is in the form
ax² + bx + c = 0 where a, b, and c are integers, you can go straight to the answer by simply plugging your values for a, b, and c into the quadratic formula
 over 2a.
over 2a.
It's great to memorize this formula as it is used in many problems.
I have also attached my work in the image provided.