Question

Consider the function f(x)=3x-1 (over)x+4 (a) At which value of x will the function not have a solution? Explain your answer. (b) If g(x) is a vertical shift of 4 units of f(ax), write the function of g(ax). How does the graph 3. Consider the function f(x) of g(x) compare to the graph of f(x)? Explain the function you wrote. (e) What is the value of x when g(x) 8? Show your work. PLEASE HELP ITS DUE

Answer 1

Ans(a):

Given function is
`f(x)=(3x-1)/(x+4)`

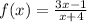
we know that any rational function is not defined when denominator is 0 so that means denominator x+4 can't be 0

so let's solve

x+4≠0 for x

x≠0-4

x≠-4

Hence at x=4, function can't have solution.

Ans(b):

We know that vertical shift occurs when we add something on the right side of function so vertical shift by 4 units means add 4 to f(x)

so we get:

g(x)=f(x)+4

`g(x)=(3x-1)/(x+4)+4`

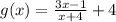
We may simplify this equation but that is not compulsory.

Comparision:

Graph of g(x) will be just 4 unit upward than graph of f(x).

Ans(e):

To find value of x when g(x)=8, just plug g(x)=8 in previous equation

`8=(3x-1)/(x+4)+4`

`8-4=(3x-1)/(x+4)`

`4=(3x-1)/(x+4)`

`4(x+4)=(3x-1)`

`4x+16=3x-1`

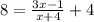
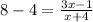
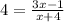
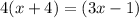
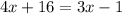
4x-3x=-1-16

x=-17

Hence final answer is x=-17