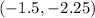Solve the system of equations below by graphing. x^2-2x+y-3=0 x^2+y=0 What is the solution rounded to the nearest hundredth? (–2.25, –1.5) (–1.5, –2.25) (–0.82, –0.68) (–0.68, –…

Question

asked Sep 6, 2019 206k views

2 Answers

Garbo · Answer 1 · 2019-09-11T09:11:14+0000

ANSWER

The correct answer is B

EXPLANATION

The first function is

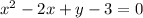
x^2-2x+y-3=0

We make y the subject to obtain;

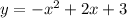
y=-x^2+2x+3

Let us quickly write this in the vertex form.

y=-(x^2-2x)+3

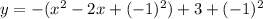
y=-(x^2-2x+(-1)^2)+3+(-1)^2

y=-(x-1)^2+4

Since the
is negative, the graph opens up.

The vertex is at
(1,4)

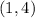
The y-intercept is

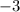
The x-intercept is found by equating the function to zero.

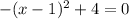
-(x-1)^2+4=0

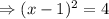
$\Rightarrow (x-1)^2=4$

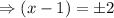
$\Rightarrow (x-1)=\pm 2$

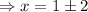
$\Rightarrow x=1 \pm2$

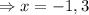
$\Rightarrow x=-1,3$

With these information we can quickly sketch the graph as shown in the attachment(the red graph).

For the second function,

x^2+y=0

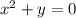
we again make y the subject to obtain,

y=-x^2

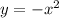
This is a basic quadratic function that can be graphed easily. Note that it is also a maximum graph.

From the graph the solution to the two functions is

(-1.5,-2.25)