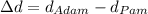Answer:
To solve this problem, we need to use the following formula
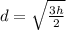
Where
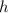 is the eye-level height and
is the eye-level height and
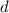 is the horizontal distance to the horizon.
is the horizontal distance to the horizon.
For Pam, we know that
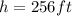 ,
,
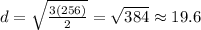
She can see around 19.6 feet to the horizon.
For Adam, we know that
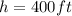
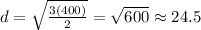
He cansee around 24.5 feet to the horizon.
Now, the difference is
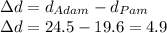
Therefore, Adam can see 4.9 feet much farther than Pam.
Additionally, the expression that models this situation is