Question

A yogurt shop allows its customers to add, for no charge, 3 toppings to any yogurt purchased. If the store has 15 possible toppings, how many different 3-topping combinations can a customers choose?

Answer 1

only 455

Explanation:

i have a ? how do you know when its C(n,r) and not P(n,r)

Answer 2

Question says that a yogurt shop allows its customers to add, for no charge, 3 toppings to any yogurt purchased. Also the store has 15 possible toppings.

Now we need to find about how many different 3-topping combinations can a customers choose.

To find that we just need to apply combination formula

`C(n,r)=(n!)/(r!(n-r)!)`

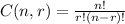
which is used to select r items out of n items

we have to find combination of 15 toppings into 3 toppings so we calculate C(15,3) using above formula

`C(15,3)=(15!)/(3!(15-3)!)`

`C(15,3)=(15!)/(3!*12!)`

`C(15,3)=(15*14*13*12!)/(3!*12!)`

`C(15,3)=(15*14*13)/(3!)`

`C(15,3)=(2730)/(6)`

`C(15,3)=455`

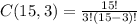
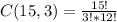
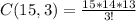
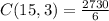
Hence final answer is 455.