Question

A farmer has a collapsable grain bag which can expand both vertically and horizontally as he needs it to. He wants to find a function to represent how much grain he can put in bag based on how much he has expanded it. When the bag is laying flat on the ground the area can be represented by the function f(x) = 3x2 + 1 and as the bag is raised up the height can be represented by the function g(x) = x+ 5. In terms of x, how much grain can the bag hold?

Answer 1

`3x^(3)+15x^(2)+x+5`

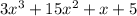
Explanation:

We are told that the area of the bag can be represented by the function
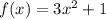`f(x)=3x^(2) +1` and as the bag is raised up its height can be represented by the function
`g(x)=x +5`.

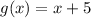Since we know that we can find volume of cuboid by multiplying base area to its height. We are given area and height of bag as functions. Now we will find volume of the bag by multiplying these functions.

`\text{Volume of collapsible bag}=f(x)*g(x)`

`\text{Volume of collapsible bag}=(3x^(2)+1)*(x +5)`

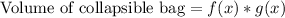
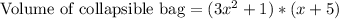
After using distributive property we will get,

`\text{Volume of collapsible bag}=3x^(2)(x+5)+1(x+5)`

`\text{Volume of collapsible bag}=3x^(3)+15x^(2)+x+5`

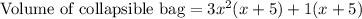
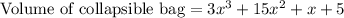
Therefore, the collapsible bag can hold
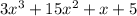`3x^(3)+15x^(2)+x+5` grain.