Question

Write the quadratic function in vertex form. Y = x2 + 16x + 74

Answer 1

The vertex form of the given quadratic function is,

`\boxed {\boxed {y = (x+8)^2+10}}`

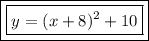
Solution-

The equation for a parabola or quadratic function can be written in vertex form-

`y=a(x-h)^2+k`

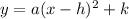
The given quadratic function,

`\Rightarrow y = x^2 + 16x + 74`

`\Rightarrow y = (x)^2 + (2* x * (16)/(2)) + 74`

`\Rightarrow y = (x)^2 + (2* x * 8) + 74`

`\Rightarrow y = (x)^2 + (2* x * 8) + (8)^2+74-8^2`

`\Rightarrow y = (x+8)^2+74-64`

`\Rightarrow y = (x+8)^2+10`

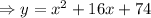
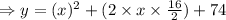
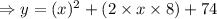
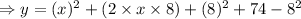
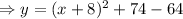
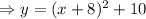
This is the vertex form of the given quadratic function with vertex at (-8, 10)