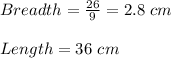Question

The length of a rectangular board is 10 centimeters longer than its width. The width of the board is 26 centimeters. The board is cut into 9 equal pieces. A: What is the area of each piece B: What are the possible dimensions of each piece?( Take the dimensions to be whole numbers ) What are the steps.

Answer 1

Answer: Area of each piece = 104 cm² and the possible dimensions of each piece will be

1) Length=4 cm and Breadth = 26 cm

2) Length=36 cm and Breadth = 2.8 cm.

Explanation:

Since we have given that

Width of rectangle = 26 cm

Since length is 10 cm longer than its width ,

So, Length of rectangle = 26+10=36 cm

Area of rectangle is given by

`Area=Length* breadth\\\\Area=36* 26\\\\Area=936\ cm^2`

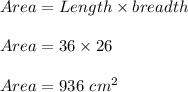
Now, we have given that the board is cut into 9 equal pieces ,

So, Area of each piece is given by

`Area\ of\ each\ piece=\frac{\text{Area of board}}{9}\\\\Area\ of\ each\ piece=(936)/(9)\\\\Area\ of\ each\ piece=104\ cm^2`

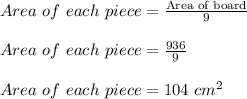
Now, the possible dimensions of each piece will be

If we cut along the length then

`Length=(36)/(9)=4\\\\Width=26`

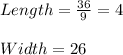
If we cut along the breadth then

`Breadth=(26)/(9)=2.8\ cm\\\\Length=36\ cm`

Answer 2

Let w be the width of the rectangular board

Let l be the length of the rectangular board.

Given that w = 26cm

∴ l = 26 + 10 = 36cm [∵ length is 10cm longer than width]

Now the board can be cut into 9 equal pieces, each of length 4cm along the length of the board [∵ 9 × 4 = 36]

The width of each of the 9 pieces will remain 26cm.

Answer A : area of each piece is

A = l × w = 4 × 26 =

Answer B : dimension of each piece is

l = 4 cm

w = 26 cm