Question

Let f(x) represent a function. Which descriptions match the given transformations? Drag and drop the answers into the boxes.

Answer 1

The correct answers are:

1. f (x) is translated 4 units down.

2. f (x) is vertically stretched by a factor of 4.

I took the quiz and these were the right answers. Hope I helped! <3

Answer 2

`f(x)-4\rightarrow` f(x) is translated 4 units down

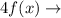`4f(x)\rightarrow` f(x) is vertically stretched by a factor of 4

Explanation:

We are given that a function f(x).

We have to match the given transformation with its correct descriptions.

We know that

When a function is translated 4 units up by the rule of transformation

is given by

`f(x)\rightarrow f(x)+4`

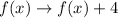
When a function is translated 4 units left by the rule of transformation

is given by

`f(x)\rightarrow f(x+4)`

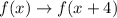
When a function is vertically stretched by a factor of 4 then it is transformed by the rule is given by

`f(x)\rightarrow 4f(x)`

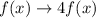
When a function is translated 4 units right by the rule of transformation

is given by

`f(x)\rightarrow f(x-4)`

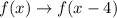
When a function is translated 4 units down by the rule of transformation

is given by

`f(x)\rightarrow f(x)-4`

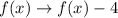
When a function is vertically compressed by a factor of 4 then it is transformed by the rule is given by

`f(x)\rightarrow (1)/(4)f(x)`

Therefore,
`f(x)-4\rightarrow` f(x) is translated 4 units down

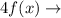`4f(x)\rightarrow` f(x) is vertically stretched by a factor of 4