Question

find zeros and y intercept and describe the end behavior in proper notation. then sketch the graph. 3x^3+2x^2-12x-8

Answer 1

Answer: The zeros of the given equation are 2, -2 and -0.667. The y-intercept of the graph is f(0) = -8.

Step-by-step explanation:

The given expression is,

`f(x)=3x^3+2x^2-12x-8`

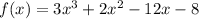
To find zeros put f(x)=0

`3x^3+2x^2-12x-8=0`

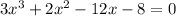
This equation is satisfied by x=2, so (x-2) is the factor of the given equation. By synthetic division or long division we can find the remaining factor.

`(x-2)(3x^2+8x+4)=0`

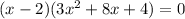
Use Factoring method.

`(x-2)(3x^2+6x+2x+4)=0`

`(x-2)(3x(x+2)+2(x+2)=0`

`(x-2)(3x+2)(x+2)=0`

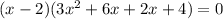
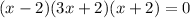
Equate each factor equal to zero by using zero product property.

So the zeros of the given equation are 2, -2 and -0.667.

To find the y-intercept of the graph, put x=0.

`f(0)=3(0)^3+2(0)^2-12(0)-8`

`f(0)=-8`

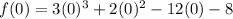
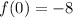
So the y-intercept of the graph is f(0) = -8.

Since the higher degree is 3 , which is odd and the coefficient of higher degree is positive, therefore the ead behavior is defined as,

`f(x)\rightarrow \infty \text{ as }\rightarrow \infty\\f(x)\rightarrow -\infty \text{ as }\rightarrow -\infty`

It means as x decreases unboundedly then the function decreases unboundedly. similarly x increases unboundedly then the function increases unboundedly.