Question

The table shows the input and output of a function Table(input:3,4,6,11. Output:5,7,11,21) (a) Explain what makes this set of data a function. (B) what could cause this set of data to not be a function? Provide a specific example to support your statement and explain throughly. (c) write an equation, in function nation, that would fit in the inputs and outputs in the table. Show your work that proves your equation is true for the given data. PLEASE HELP ITS DUE TODAY!!!

Answer 1

Ans(a):

We know that a function can't have repeated x-values.

In given table we see that there i no repeating x-value. That's why the given table represents function.

Ans(b):

We know that a function can't have repeated x-values.

So if in given table we see any repeating x-value then that may cause the given data set to not be a function.

like if we have 3, 4, 3, 11 in the input then it will not be a function.

Ans(c):

we can use two points say (3,5) and (4,7) to find the linear equation of the form y=mx+b

slope is given by

`m=(y_2-y_1)/(x_2-x_1)=(7-5)/(4-3)=2`

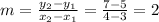
Noow plug value of m=2 and any point say (3,5) into y=mx+b

5=2(3)+b

5=6+b

-1=b

now plug m=2 and b=-1 in y=mx+b, we get y=2x-1

Hence required equation in function notation can be written as

f(x)=2x-1.

Now to prove that above function is correct, we just graph the given points from table and the obtained function.

We see that points lie on the grpah of f(x)=2x-1.

Which proves that our equation is correct.