Answer:
The domain of the function is the set of all the real values except x=0
i.e. the domain: (-∞,∞)-{0}
Explanation:
The domain of a function is the set of all the x-values for which the function is defined.
We are given a function f(x) in the form as:
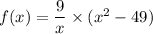
Hence, the function f(x) is defined everywhere except the point where the denominator is zero.
Hence, we see that the denominator of f(x) is " x "
which is zero only when x=0
Hence, the domain of the function f(x) is the set of all the real values except x=0.