Answer:
Gravitational potential energy:

Kinetic energy:
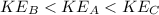
Total mechanical energy:
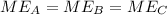
Step-by-step explanation:
The gravitational potential energy is directly proportional to height (
 ). Since there are no non-conservative forces, the total mechanical energy is conserved (
). Since there are no non-conservative forces, the total mechanical energy is conserved (
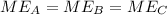 ) and the total mechanical energy is the sum of gravitational potential and kinetic energies. Then:
) and the total mechanical energy is the sum of gravitational potential and kinetic energies. Then:
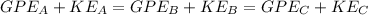 (1)
(1)
If we know that
 , then we conclude the following inequation for the kinetic energy:
, then we conclude the following inequation for the kinetic energy:
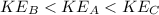 (2)
(2)