Question

Factor the expression completely over the complex numbers.


`y^(4)+40y^(2)+400`

Answer 1

The answer is [y² + 20]² because using the "Greatest Common Factor" strategy, you'll have this below:

(y^4 + 20y²) + (20y² + 400)

y²(y² + 20) 20(y² + 20)

[y² + 20][y² + 20] = [y² + 20]²

Sorry it took so long. I was trying to figure out the code for the 4th power exponential. I never take this long to answer any mathematical question. Please forgive me?

Answer 2

`(y^2+20)^2`

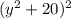
Explanation:

Consider the given expression

`y^4+40y^2+400`

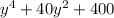
We need to find the factor form of the given expression.

Splitting the middle term, rewrite the middle term as
`20y^2+20y^2`.

`y^4+20y^2+20y^2+400`

`(y^4+20y^2)+(20y^2+400)`

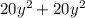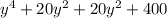
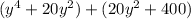
Taking out common factors from each parenthesis.

`y^2(y^2+20)+20(y^2+20)`

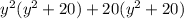
Taking out common factors.

`(y^2+20)(y^2+20)`

`(y^2+20)^2`

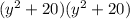
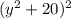
Therefore, the factored form of given expression is
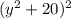`(y^2+20)^2`.