For artificial gravity the the position of rim we have to rotate the space station
Due to rotation it will experience centripetal acceleration at the position of rim
Now in order to experience this acceleration to be same as gravity we can say centripetal acceleration must be equal to gravity here
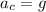
as we know that centripetal acceleration is given as


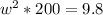
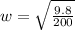
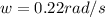
now we know that angular frequency will be related to time period as
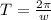
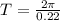
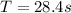
so it will rotated by time period T = 28.4 s