Question

The equation y=470x represents the relationship between x, the time that a plane flies in hours, and y, the distance the plane flies in miles for plane A. The table represents the relationship for plane B. Find the slope of the graph for each plane and the plane's rate of speed. Determine which plane is flying at a faster rate of speed look at the picture please

Answer 1

Plane A:

The rate of change or slope of function A is: m = 470

It means plane A is flying 470 miles per hour.

Thus, the rate of speed of plane A is 470 miles per hour.

Plane B:

The rate of change or slope of Plane B is: m = 480

It means Plane B is flying 480 miles per hour.

Thus, the rate of speed of plane A is 480 miles per hour.

Therefore, we conclude:

• Plane B is flying faster.

Explanation:

The slope-intercept form of the line equation

`y = mx+b`

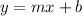
where

• m is the rate of change or slope

• b is the y-intercept

Plane A

From the given equation

y = 470x

where

x is the time that plane flies in hours

y is the distance the plane flies in miles

Thus, comparing with the slope-intercept form y = mx+b

The rate of change or slope = 470

It means plane A is flying 470 miles per hour.

Plane B

Given the table

Time (h) 1 2 3 4

Distance (mi) 480 960 1440 1920

Finding the slope by taking any two points, let say, (1, 480) and (2, 960)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(1,\:480\right),\:\left(x_2,\:y_2\right)=\left(2,\:960\right)`

`m=(960-480)/(2-1)`

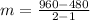
Refine

`m=480`

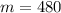
Therefore, the rate of change or slope of Plane B is: m = 480

It means Plane B is flying 480 miles per hour.

Conclusion:

Plane A:

The rate of change or slope of function A is: m = 470

It means plane A is flying 470 miles per hour.

Thus, the rate of speed of plane A is 470 miles per hour.

Plane B:

The rate of change or slope of Plane B is: m = 480

It means Plane B is flying 480 miles per hour.

Thus, the rate of speed of plane A is 480 miles per hour.

Therefore, we conclude:

• Plane B is flying faster.