Question

A helicopter flies 250 km on a straight path in a direction 60° south of east. The east component of the helicopter’s displacement is km.

Answer 1

125km

Step-by-step explanation:

the east component is given by the cosine function of the given angle.

because of the triangle that is formed between the east component end the south-east component

`cos\theta=(adjacent Leg)/(hypotenuse)`

in this case the angle is:
`\theta =60`

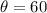
the adyacent Leg is the east component
`Ec`

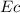
and the hypotenuse:
`d=250km`

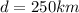
so:

`cos60=(Ec)/(250km)`

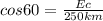
we clear for the east component:

`Ec=(250km)(cos60)\\Ec=(250km)(0.5)\\Ec=125km`

you can see the the triangle in the attached image, where the blue line is the east component

Answer 2

Given that,

Distance in south-west direction = 250 km

Projected angle to east = 60°

East component = ?

since,

cos ∅ = base/hypotenuse

base= hyp * cos ∅

East component = 250 * cos 60°

East component = 125 km