Question

Line AB passes through points A(-6,6) and B(12, 3) If the equation of the line is written in slope-intercept form, y then m1 and b mx+ b, then m=-1/6 and b =?

Answer 1

The value of b is 5.

Explanation:

Given: Line AB passes through points A(-6,6) and B(12,3).

Slope- intercept form:-The equation of a line with slope m and making an intercept b on y -axis is y = mx + b.

Since the line passes through two points therefore, we can use the Two Point Form formula:

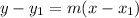`y-y_(1)=m(x-x_(1))` ; where m is the slope.

or Slope
`m =(y_(2)-y_(1))/(x_(2)-x_(1))`

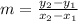
First find the value of m using the points A(-6,6) and B(12,3) ;

`m = (3-6)/(12-(-6)) = (-3)/(18) =(-1)/(6)`

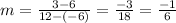
Now, the equation of line AB :-

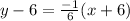`y-6=(-1)/(6)(x+6)` or

`y-6 =(-1)/(6) x-(6)/(6)` or

`y-6=(-1)/(6) x-1` or

`y=(-1)/(6)x-1+6`

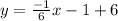
Simplify:

`y = (-1)/(6)x+5`

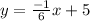
Comparing above equation with the general equation of line i.e, y = mx+b , we get;

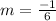`m= (-1)/(6)` and b= 5

Therefore, the value y-intercept (b) = 5