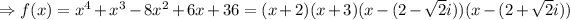ANSWER TO QUESTION 1
Check attachment for long division.
From our long division we can write the following;
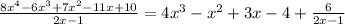
Since the polynomial
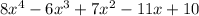 leaves a non zero remainder of
leaves a non zero remainder of
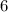 when divided by
when divided by
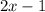 , we conclude that
, we conclude that
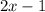 not a factor of the dividend,
not a factor of the dividend,
ANSWER TO QUESTION 2
We want to factor
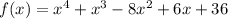
The possible rational roots are;
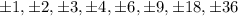
We found
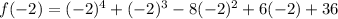

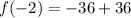

and
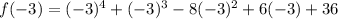
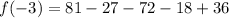

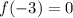 .
.
This means that
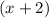 and
and
 are factors of the polynomial.
are factors of the polynomial.
This also means that
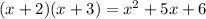 is also a factor of the polynomial
is also a factor of the polynomial
So we apply long division to obtain the remaining factors as shown in the attachment.
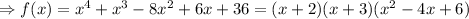
We factor further to obtain;