Question

Write the equation of the perpendicular bisector of AB

Answer 1

As the name suggests, the perpendicular bisector of a given segment is a line that is perpendicular to the given one and passes through its midpoint.

Remember that, if a line has slope m, a perpendicular line will have slope k, such that mk = -1.

Step 1: Slope of AB

We compute the slope with the usual formula

`m = (\Delta y)/(\Delta x) = (A_y-B_y)/(A_x-B_x) = (7-2)/(1-4) = (5)/(-3) =-(5)/(3)`

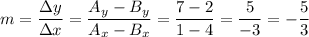
Step 2: Perpendicular Slope

We're looking for a slope k such that

`-(5)/(3)k=-1 \iff (5)/(3)k=1 \iff k = (3)/(5)`

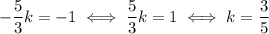
Step 3: Midpoint of AB

The coordinates of the midpoint are the average of the coordinates of the endpoint. So, the midpoint M has coordinates

`M_x = (1+4)/(2) = (5)/(2),\quad M_y = (2+7)/(2) = (9)/(2)`

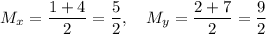
So, the midpoint is (5/2,9/2)

Step 4: line equation

If you know the slope of a line, and a point belonging to it, the equation of the line is given by

`y-y_0 = m(x-x_0)`

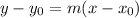
Plug your values:

`y-(9)/(2) = (3)/(5)\left(x-(5)/(2)\right)`

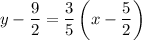
Which you can rearrange as

`y = (3x)/(5) + 3`