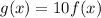Answer:
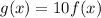
Explanation:
We know that when we vertically stretch the graph of a function h(x) by sacle factor of m, then the new function will becomes :-
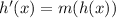
Similarly, if the graph of function g is a vertical stretch of the graph of function f by a factor of 10, then the equation of new function g is given by :-
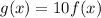
Thus, the equation describes function g is