Question

Ms. Waller receives orders for posy bouquets and cascade bouquets. It usually takes her 15 minutes to make one posy bouquet and 20 minutes to make one cascade bouquet. For today's orders, each posy bouquet must have 12 stems and each cascade bouquet must have 6 stems. Ms. Waller has no more than 300 minutes to make the bouquets, and she can procure no more than 180 stems in all. Ms. Waller makes a profit of $10 on each posy bouquet and $7 on each cascade bouquet. How many posy bouquets and cascade bouquets should she deliver to maximize her profit?

Answer 1

Answer: Ms. Waller should deliver 12 posy bouquet and 6 cascade bouquets.

Step-by-step explanation:

Let the number of delivered posy bouquet be x and The number of delivered cascade bouquets be y. So,
`x\geq 0,y\geq 0`

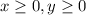
It is given that it usually takes her 15 minutes to make one posy bouquet and 20 minutes to make one cascade bouquet. Ms. Waller has no more than 300 minutes to make the bouquets.

`15x+20y\leq 300`

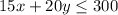
For today's orders, each posy bouquet must have 12 stems and each cascade bouquet must have 6 stems and she can procure no more than 180 stems in all.

`12x+6y\leq 180`

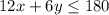
Ms. Waller makes a profit of $10 on each posy bouquet and $7 on each cascade bouquet.

`Z=10x+7y`

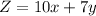
So we have to maximise the value of Z.

Subject to the constants,

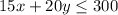`1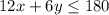5x+20y\leq 300` ..... (1)

`12x+6y\leq 180` ..... (2)

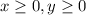`x\geq 0,y\geq 0` .... (3)

Plot these inequalities on a coordinate plane as shown below.

Solve equation (1) and (2) by elimination method to find the intersection point of both lines.

On solving (1) and (2), we get x=12 and y=6.

The vertex of shaded region are (0,0),(15,0),(12,6) and (0,15).

Check the value of Z on each vertex.

The value of Z are 0,150,162 and 105 on (0,0),(15,0),(12,6) and (0,15) respectively.

Therefore, the maximum profit is 162 on (12,6). It means Ms. Waller should deliver 12 posy bouquet and 6 cascade bouquets to maximise her profit.