Answer:
The correct option is: B. 9
Explanation:
The number of tennis balls,
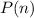 , in
, in
 layers of the square pyramid is given by:
layers of the square pyramid is given by:
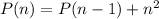
As the stack of the tennis balls is in shape of a square pyramid, that means in the top layer, there will be one ball. So,
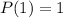
Now, if
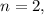 then
then
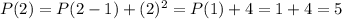
If
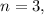 then
then
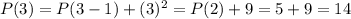
If
 then
then
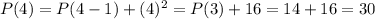
That means, the number of tennis balls from the top layer will be: 1, 5, 14, 30, .......
So, the number of tennis balls that Coach Kunal could not have is 9.