Answer:
Section A has 25,000 seats.
Section B has 14,800 seats.
Section C has 10,200 seats.
Explanation:
Let the seats in section A be = x
Let the seats in section B be = y
Let the seats in section C be = z
The equations forms as follows:
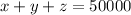 .....(1)
.....(1)
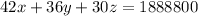 .......(2)
.......(2)
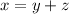 ......(3)
......(3)
Substituting the value of x in (1) to get equation in two terms.
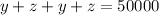
=>
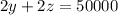
taking out 2 common, we get;
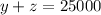 .........(4)
.........(4)
And substituting the value of x in (2), we get
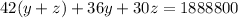
=>

=>
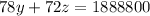
Taking out 2 common, we get;
 ........(5)
........(5)
Multiplying (4) by 39 and subtracting (5) from (4), we get
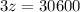
We get z = 10200
And
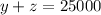
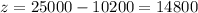
We get y = 14800
Also
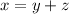
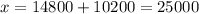
We get x = 25000
Therefore,
Section A has 25,000 seats.
Section B has 14,800 seats.
Section C has 10,200 seats.