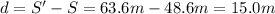Question

You are driving at the speed of 27.7 m/s (61.9764 mph) when suddenly the car in front of you (previously traveling at the same speed) brakes and begins to slow down with the largest deceleration possible without skidding. Considering an average human reaction, you press your brakes 0.543 s later. You also brake and decelerate as rapidly as possible without skidding. Assume that the coefficient of static friction is 0.804 between both cars’ wheels and the road.

Calculate the acceleration of the car in front
of you when it brakes.
Calculate the braking distance for the car in
front of you.
Find the minimum safe distance at which you
can follow the car in front of you and avoid
hitting it (in the case of emergency braking
described here).

Answer 1

1) Acceleration of the car in front: -7.89 m/s^2

The only data we need for this part of the problem is:

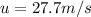`u = 27.7 m/s` --> initial velocity of the car

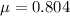`\mu=0.804` --> coefficient of friction between the car wheels and the road

From the coefficient of friction, we can find the deceleration of the car. In fact, the force of friction is given by

`F=-\mu mg`

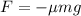
where m is the car's mass and
`g=9.81 m/s^2` is the acceleration due to gravity. We can find the car's acceleration by using Newton's second law:

`a=(F)/(m)=(-\mu mg)/(m)=\mu g=(0.804)(9.81 m/s^2)=-7.89 m/s^2`

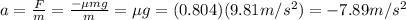
And the negative sign means it is a deceleration.

2) Braking distance for the car in front: 48.6 m

This can be found by using the following SUVAT equation:

`v^2 - u^2 = 2aS`

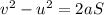
where

v=0 is the final velocity of the car

u=27.7 m/s is the initial velocity of the car

a=-7.89 m/s^2 is the acceleration of the car

S is the braking distance

By re-arranging the formula, we find S:

`S=(v^2-u^2)/(2a)=(0-(27.7 m/s)^2)/(2(-7.89 m/s^2))=48.6 m`

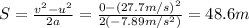
3) Minimum safe distance at which you can follow the car: 15.0 m

In this case, we must calculate the thinking distance, which is the distance you travel before hitting the brakes. During this time, the speed of your car is constant, so the thinking distance is given by

`d_t = ut=(27.7 m/s)(0.543 s)=15.0 m`

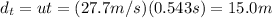
After hitting the brakes, your car decelerates at the same rate of the car in front of you, so the braking distance is the same of the other car:

`d_b=48.6 m`

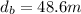
So the total distance your car covers is

`S'=d_t+d_b=15.0 m +48.6 m=63.6 m`

At the same time, the car in front of you just covered a distance of 48.6 m. So, in order to avoid the collision, you should travel at a distance equal to

`d=S'-S=63.6 m-48.6 m=15.0 m`