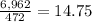Question

The table of values represents a function ​f(x).

How much greater is the average rate of change over the interval [9, 10] than the interval [5, 8] ?



Enter your answer in the box.

Answer 1

6490

Explanation:

correct answer just took test and they give correct answers when they grade them

Answer 2

- The interval [9, 10] is 1,375% greater than the interval [5, 8].

- The interval [9, 10] is 14.75 times greater than the interval [5, 8].

Explanation:

1. To solve this problem you must apply the following formula:

`AverageRateOfChange=(y_(2)-y_(1))/(x_(2)-y_(1))`

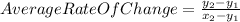
2. Let's calculate the average rate of change of each interval:

a) Interval [9,10]:

`=(11,014-4,052)/(10-9)=6,962`

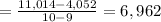
b) Interval [5,8]:

`=(1,491-75)/(8-5)=472`

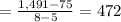
3. The difference is:

`6,962-472=6,490`

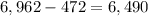
4. In percentage:

`((6,962-472)/(472))(100)=1,375%`

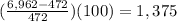
5. You have that the interval [9,10] is 14.75 times greater than the interval [5,8], as you can see below:

`(6,962)/(472)=14.75`