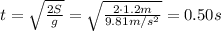Question

A raccoon falls out of a tree from a height of 1.2. Which equation can you use to calculate the time it takes for the raccoon to fall to the ground?

Answer 1

Δd = 1/2aΔt²+v₁Δt

Step-by-step explanation:

Just did it on A.pex

Answer 2

`t=\sqrt{(2S)/(g)}=\sqrt{(2 \cdot 1.2 m)/(9.81 m/s^2)}=0.50 s`

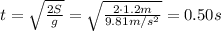
Step-by-step explanation:

The equation that we can use to calculate the time it takes for the raccoon to fall to the ground is:

`t=(2S)/(g)`

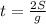
where S=1.2 m is the height of the tree and g=9.81 m/s^2 is the acceleration due to gravity. This equation is derived from the equation of the distance in a uniformly accelerated motion, which is given by

`S=S_0 + v_0 t + (1)/(2)at^2`

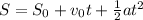
where S0 is the initial position, v0 is the initial velocity and t the time. In this problem, we can put S0=0 (we can take the initial position as the initial position of the raccoon) and v0=0 (the raccoon starts from rest), so the equation becomes

`S=(1)/(2)at^2`

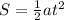
and since the motion is a free fall, the acceleration is equal to the acceleration of gravity, so a=g:

`S=(1)/(2)gt^2`

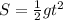
And by re-arranging it, we find

`t=\sqrt{(2S)/(g)}`

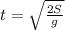
By substituting numbers, we find

`t=\sqrt{(2S)/(g)}=\sqrt{(2 \cdot 1.2 m)/(9.81 m/s^2)}=0.50 s`