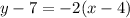Question

A line with a slope of -2 passes through the point (4, 7). Write an equation for this line in point-slope form.

Answer 1

`\bf (\stackrel{x_1}{4}~,~\stackrel{y_1}{7})~\hspace{10em} slope = m\implies -2 \\\\\\ \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-7=-2(x-4)`

Answer 2

The equation in point-slope is
`y-7=-2(x-4)`.

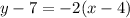Explanation:

Point-slope is a specific form of linear equations in two variables:

`y-b=m(x-a)`

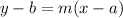
When an equation is written in this form, m gives the slope of the line and (a, b) is a point the line passes through.

We want to find the equation of the line that passes through (4, 7) and whose slope is -2. Well, we simply plug m = -2, a = 4, and b = 7 into point-slope form.

`y-7=-2(x-4)`