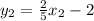For this case we have to;
We have that an equation in slope-intercept form is given by:
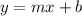
Where:
m is the slope
b is the cut point with the y axis
Also, by definition, two lines are perpendicular when the product of their slopes is -1. That is:
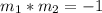
We have the line as data:

Then
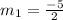
We found
 :
:
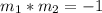
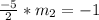
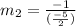
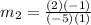
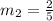
Thus,
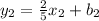
We must find
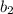 :
:
We know that
 passes through the point
passes through the point
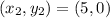
We substitute the point in the equation of
 :
:
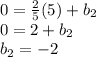
Thus,
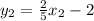
Then the equation in slope-intercept for the line that passes through (5,0) and is perpendicular to the line described by
 is:
is:
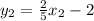
Answer: